[Numpy] #11 np.deg2rad(), np.rag2deg(), np.np.e, np.pi, np.sin(), cos(), tan(), / 수학에서 사용되는 개념, 상수 기본문법 공부하기 11

포스팅 제목을 보면, 머리가 하얘진다... 수학 다 까먹은 문과 놈이 요것들 정리하려면, 수학 포스팅할게 많아지겠다.

메소드 활용은 간단하나.. 결과를 이해하고, 연산에 활용하기 위해선 개념 공부가 필수적이겠다! 하나하나 포스팅해가면서 나아가 보겠다! 화이팅

 

1. np.deg2rad(), np.rad2deg()

np.deg2rad(), np.rad2deg()는 "각도법 to 호도법", "호도법 to 각도법"으로 서로 방식으로 값을 변환하는 메소드이다. 

호도법, 각도법 특히, 호도법에 대한 설명을 포스팅으로 작성해보았다.

https://doyou-study.tistory.com/65

[수학] 라디안과 각도와의 관계 / radian와 degree

 

호도법을 알고 있거나,,, 포스팅을 읽고 왔다면 관련한 코드를 작성해보도록 하겠다.

 

import numpy as np

degree = np.array([30, 45, 60, 90, 180, 360])
rad = np.deg2rad(degree)
degree = np.rad2deg(rad)

print(rad.round(3)) # [0.524 0.785 1.047 1.571 3.142 6.283]
print(degree) # [ 30.  45.  60.  90. 180. 360.]

pi = np.pi
rad = np.array([pi/6, pi/4, pi/3, pi/2, pi, 2*pi])
degree = np.rad2deg(rad)

print(rad)  # [0.52359878 0.78539816 1.04719755 1.57079633 3.14159265 6.28318531]       
print(degree)   # [ 30.  45.  60.  90. 180. 360.]

기본적으로

np.deg2rad(): 각도를 라디안으로 변환

np.rad2deg(): 라디안을 각도로 변환

을 의미한다.

 

그래서 degree 변수에 대표적인 각도를 집어넣고,

np.deg2rad(degree)을 수행하면, 각각의 각도가 라디안 값으로 변환된다.

변환이 수행된 rad를 출력해보면, 밑의 표의 라디안 값을 실수로 표현한 것뿐, 값은 동일하게 출력된다.

똑같이 rad변수에 대표적인 라디안 값을 집어넣고,

np.rad2deg(rad)을 수행하면, 각각의 라디안이 각도 값으로 변환된다.

실제 값을 확인해보면, 각각의 라디안 값이 각도 값으로 변환된 것을 확인할 수 있다.

 

라디안	각도
π/6	30°
π/4	45°
π/3	60°
π/2	90°
π	180°
2π	360°

 

 

2. np.sin(), np.cos(), np.tan(), np.sinh(), np.conh(), np.tanh()

2.1 np.sin(), np.cos(), np.tan()

np.sin(), np.cos(), np.tan()에 대해 먼저 알아보겠다.

np.sin(), np.cos(), np.tan()는 말 그대로 sinθ, cosθ, tanθ를 리턴하는 메소드이다.

sin, cos, tan가 무엇인지 먼저 알아보도록 하겠다. 관련 포스팅을 간단하게 작성해봤다.

https://doyou-study.tistory.com/66

삼각함수의 기본 - sin cos tan의 정의와 주기/ 사인, 코사인, 탄젠트에 대한 간단한 정리

위 포스팅을 통해 대강 sin, cos, tan에 대해서 알아봤다, 코드로 어떻게 사용하는지 살펴보자.

 

import numpy as np

degree = np.array([0, 30, 45, 90, 180, 360])
radian = np.deg2rad(degree)

sin, cos = np.sin(degree), np.cos(degree)
tan = np.tan(degree)

print(degree)   # [  0  30  45  90 180 360]

# degree
print(sin)  # [ 0.         -0.98803162  0.85090352  0.89399666 -0.80115264  0.95891572]
print(cos)  # [ 1.          0.15425145  0.52532199 -0.44807362 -0.59846007 -0.28369109]
print(tan)  # [ 0.         -6.4053312   1.61977519 -1.99520041  1.33869021 -3.38014041]

sin, cos = np.sin(radian), np.cos(radian)
tan = np.tan(radian)

print(radian)   # [0.         0.52359878 0.78539816 1.57079633 3.14159265 6.28318531]

# radian
print(sin)  # [ 0.00000000e+00  5.00000000e-01  7.07106781e-01  1.00000000e+00 1.22464680e-16 -2.44929360e-16]
print(cos)  # [ 1.00000000e+00  8.66025404e-01  7.07106781e-01  6.12323400e-17 -1.00000000e+00  1.00000000e+00]
print(tan)  # [ 0.00000000e+00  5.77350269e-01  1.00000000e+00  1.63312394e+16 -1.22464680e-16 -2.44929360e-16]

당연히 들어오는 값이 다르니 degree일 경우와 radian일 경우 값이 다르겠지.

근데 둘 중 뭘 써야 하지?

 

https://numpy.org/doc/stable/reference/generated/numpy.sin.html

numpy.sin — NumPy v1.21 Manual

 

Numpy 개발 문서를 보면 "radian"을 활용하도록 하고 있다.

 

관련해 코드를 작성해보면,

import numpy as np
import matplotlib.pylab as plt


x = np.linspace(0, 2 *np.pi, 201)

fig, ax = plt.subplots(figsize=(20, 20))
ax.plot(x, np.sin(x), label="sin")
ax.plot(x, np.cos(x), label="cos")
# ax.plot(x, np.tan(x), label="tan")    # 극한 표현을 못해 미출력

ax.legend()

plt.ylim(-1.5, 1.5)

plt.show()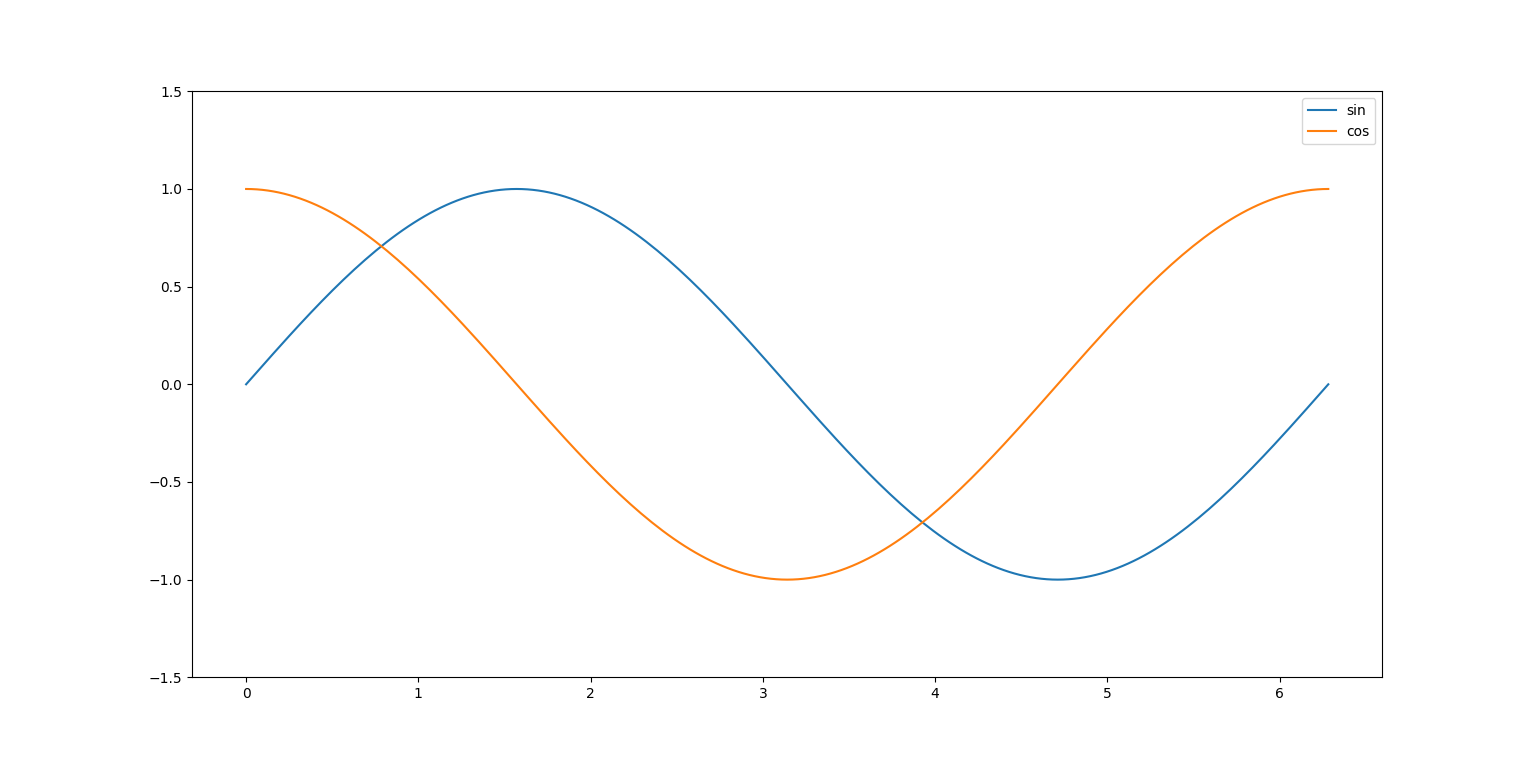

위의 삼각함수 포스팅에서 봤던 그래프가 그려진다!

 

np.sin(), np.cos(), np.tan()는 "radian" 기준임을 기억하자.

 

---

 

2.2 np.sinh(), np.cosh(), np.tanh()

np.sinh(), np.cosh(), np.tanh()는 쌍곡선 함수이다. 관련한 포스팅을 작성했다.

https://doyou-study.tistory.com/76

[수학] 쌍곡선함수, 쌍곡삼각함수 / hyperbolic function, sinh, cosh, tanh

 

관련해 코드를 작성해보고, 결과를 바라보자

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 1, 5)

sinh = np.sinh(x)
sinh_exp = (np.exp(x) - np.exp(-x)) / 2

cosh = np.cosh(x)
cosh_exp = (np.exp(x) + np.exp(-x)) / 2

tanh = np.tanh(x)
tanh_exp = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

print(sinh.round(2))
print(sinh_exp.round(2))
# [0.   0.25 0.52 0.82 1.18]
# [0.   0.25 0.52 0.82 1.18] 

print(cosh.round(2))
print(cosh_exp.round(2))
# [1.   1.03 1.13 1.29 1.54]     
# [1.   1.03 1.13 1.29 1.54] 

print(tanh.round(2))
print(tanh_exp.round(2))
# [0.   0.24 0.46 0.64 0.76]     
# [0.   0.24 0.46 0.64 0.76]

위 포스팅을 통해서 확인할 수 있듯 sinh, cosh, tanh이 sinh_exp, cosh_exp, tanh_exp의 수식임을 알 수 있다.

 

관련해 시각화해보면

import numpy as np
import matplotlib.pyplot as plt

# 시각화
x = np.linspace(-10, 10, 201)

sinh = np.sinh(x)
cosh = np.cosh(x)
tanh = np.tanh(x)

fig, ax = plt.subplots(1, 3, figsize=(20, 20))

ax[0].plot(x, sinh, label="sinh")
ax[1].plot(x, cosh, label="cosh")
ax[2].plot(x, tanh, label="tanh")

ax[0].axvline(x=0, color = 'black')
ax[0].axhline(y=0, color = 'black') 
ax[1].axvline(x=0, color = 'black')
ax[1].axhline(y=0, color = 'black') 
ax[2].axvline(x=0, color = 'black')
ax[2].axhline(y=0, color = 'black') 


ax[0].set_ylim(-20, 20)
ax[1].set_ylim(-10, 20)
ax[2].set_ylim(-5, 5)

ax[0].legend()
ax[1].legend()
ax[2].legend()


plt.show()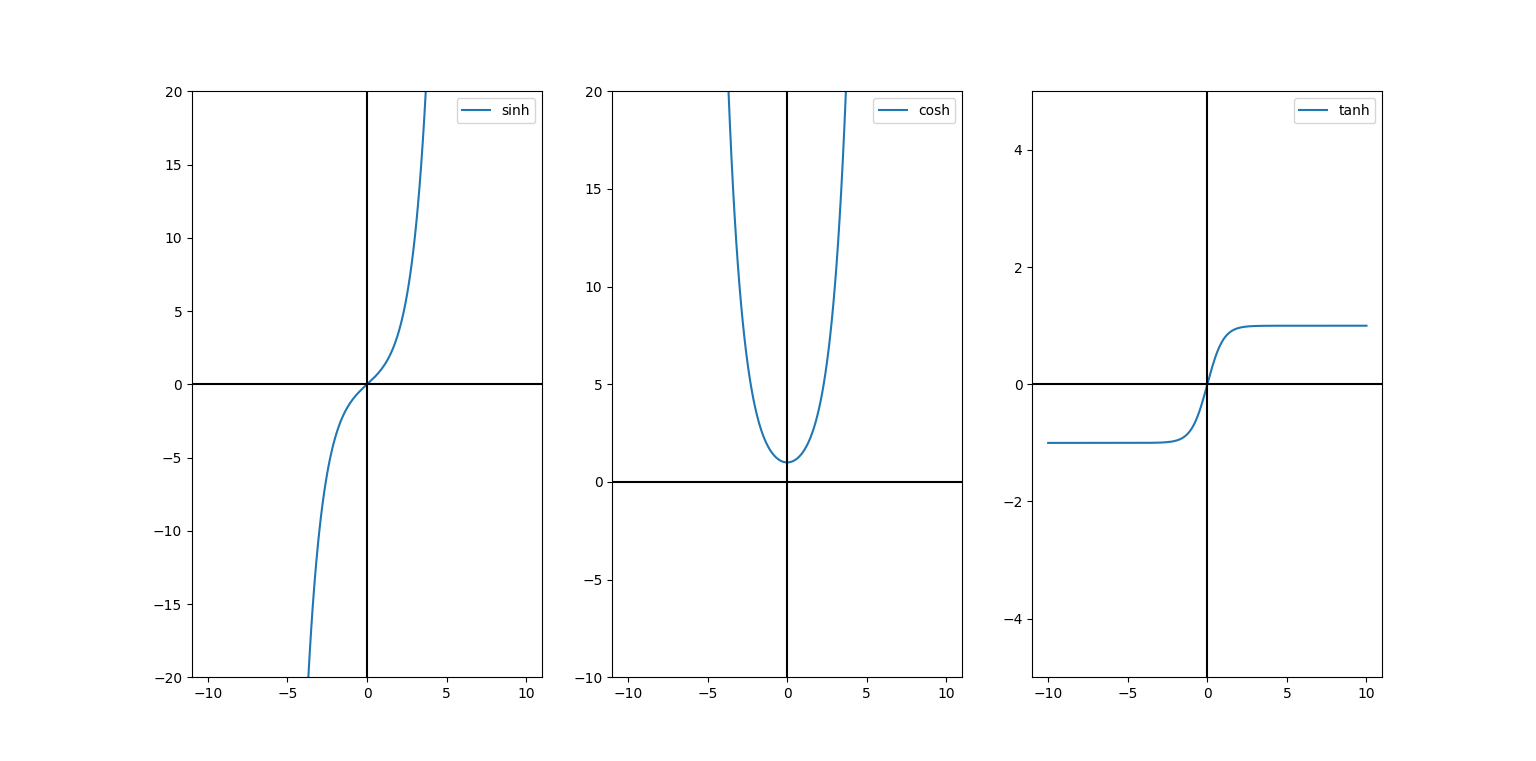

pyplot 스킬이 부족해 그림도 못그렸네ㅠ

pyplot스킬이 부족해 코드가 좀 지저분하다.

이런 식으로 Numpy 메소드를 활용하면, "sinh", "cosh", "tanh"함수를 활용할 수 있다.

 

특히 tanh함수는 딥러닝에서 활용하는 "활성화 함수"중 하나이다. 데이터에 대해서 o, x / 0, 1의 결과(할지 말지)를 연산해주는 함수 중 하나이다. 그 결과를 출력하는데, 비선형 함수인 tanh함수가 활용되고, 중요한 역할을 한다.

 

---

 

3. np.pi, np.e, np.exp(), np.log()

pi와 e는 상수이다. 다양한 방식으로 활용할 수 있다. 우리가 알고 있는 수학적 공식을 실제 코드로 작성하는 데 유용할 것이당.

 

- π

: pi, 원주율로서 "원둘레와 지름의 비"를 나타내는 수학적 상수이다.

import numpy as np

PI = np.pi

print(PI)   # 3.141592653589793

 

- e

: 문제는 요놈 자연상수이다. 

$ e\ =\ \lim\limits_{n \to \infty}{\left(1+ \dfrac 1n \right)}^n$

 

자연상수 e에 대해 검색을 해보면, 가장 일반적인 정의가 위의 수식이다.

$ {\left(1+ \dfrac 1n \right)}^n$

위 식에서 n을 계속 높여가다 보니 특정 수에 점점 수렴하는 것을 발견했고,

이 무리수를 자연상수 e로 정의한 것이다.

이 자연상수 e는 로그의 밑으로 사용돼 "자연로그" 개념을 등장시켰다.

 

실제 코드를 통해 위 식에 값을 입력해보면,

import numpy as np

n = np.array([1, 2, 5, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000])

y = np.power((1 + (1 / n)), n)

print(y)
# [2.         2.25       2.48832    2.59374246 2.70481383 2.71692393  
# 2.71814593 2.71826824 2.71828047 2.71828169 2.7182818 ]

2.71828... 의 무리수로 수렴한다. 이 값이 자연상수 e이다.

 

- np.exp()

: 포스팅을 하다 보니 위에서 벌써 사용해버렸다. 자연상수 e의 제곱을 리턴하는 메소드이다.

 

import numpy as np

e_square_1 = np.exp(2)
e_square_2 = np.e ** 2
e_square_3 = np.power(np.e, 2)

print(e_square_1)   # 7.38905609893065
print(e_square_2)   # 7.3890560989306495
print(e_square_3)   # 7.3890560989306495

위의 코드 결과처럼 자연상수 e의 제곱을 진행할 수 있다.

 

- np.log()

: 자연상수 e의 친구 log이다. Numpy 개발 문서를 확인해보면, np.log()는 기본적으로 밑을 e로 가지는 자연로그를 리턴한다.

* log에 대해선 추후에 포스팅하겠다.

 

관련된 코드를 확인해보자.

import numpy as np

a = np.array([1, np.e, np.e**2, 0])

# 밑: 자연상수 e
print(np.log(a))    # [  0.   1.   2. -inf]

# 밑: 2
print(np.log2(a))   # [0.         1.44269504 2.88539008       -inf]

# 밑: 10
print(np.log10(a))  # [0.         0.43429448 0.86858896       -inf]

코드 결과는 위와 같이 나오고 실제로 확인해보면, 같은 결과임을 알 수 있다.

 

import numpy as np

a = np.array([0, 1, 2, 3])
log = np.log(a)
exp = np.exp(log)

print(exp)  # [0. 1. 2. 3.]

 

log의 성질을 나타내는 코드를 마지막으로 해당 챕터를 마치겠다.

* log에 대해선 추후에 작성하겠습니다. 

 

 

---

4. np.reciprocal()

np.reciprocal()은 데이터의 역수를 반환한다. 여기서 역수는 "Multiplicative inverse", 0을 제외한 실수의 곱셈의 역원을 의미한다.

 

$$ a의\ 역수 =\ \frac{1}{a},\;\;a\ \times\ \frac{1}{a}\ =\ 1$$

 

import numpy as np

a = np.arange(0, 10).astype(np.float32) # int형은 a**(-1) 연산 불가
print(a)

reciprocal_1 = 1/a
reciprocal_2 = a**(-1)
reciprocal_3 = np.reciprocal(a)

print(a)
# [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]

print(reciprocal_1)
# [       inf 1.         0.5        0.33333334 0.25       0.2
#  0.16666667 0.14285715 0.125      0.11111111]

print(reciprocal_2)
# [       inf 1.         0.5        0.33333334 0.25       0.2
#  0.16666667 0.14285715 0.125      0.11111111]

print(reciprocal_3)
# [       inf 1.         0.5        0.33333334 0.25       0.2
#  0.16666667 0.14285715 0.125      0.11111111]

위에서 설명한 대로 실수들의 역수를 결과를 갖게 된다.

 

---

 

5. np.sqrt(), np.cbrt() np.power()

np.sqrt(), np.cbrt()는 데이터의 제급근, 세제곱근을 리턴하는 메소드이다.

np.power()는 데이터와의 제곱 연산을 수행하는 메소드이다.

* (제곱 값을 변수로 받기에 상황에 따라 제곱, 제곱근 연산에 유동적으로 활용될 수 있다.)

 

관련 코드로 이해해보자.

import numpy as np

a = np.random.uniform(0, 5, (4, ))

sqrt = np.sqrt(a)
sqrt_ = np.power(a, 1/2)

cbrt = np.cbrt(a)
cbrt_ = np.power(a, 1/3)

print(a)
# [4.09206866 4.48552673 0.40107439 3.87508869]
print(sqrt)
print(sqrt_)
# [2.02288622 2.11790621 0.63330434 1.9685245 ]
# [2.02288622 2.11790621 0.63330434 1.9685245 ]

print(cbrt)
print(cbrt_)
# [1.59948794 1.64919174 0.73746539 1.57070231]
# [1.59948794 1.64919174 0.73746539 1.57070231]

위와 같이 np.sqrt()과 np.cbrt()의 기능을 np.power를 통해서도 구현할 수 있다.

상황에 따라 유동적으로 사용할 수 있겠다.

 

---

 

컨디션이 안 좋아 오늘은 여기서 마무리

 

* 참조

- https://numpy.org/doc/stable/reference/generated/numpy.log.html

numpy.log — NumPy v1.21 Manual