Numpy 기본 문법 포스팅을 하다 맨입으로 설명하기 힘든 수학 개념이 나와 관련해 포스팅하려 한다.
아마 중학교 때? 배웠나 하는 "라디안"이 그것이다. 정의가 무엇인지 알아보자.
호도법의 의의, 사용하는 이유에 대해서도 알아보려 했지만, 자료를 찾아봐도 바로 이해되지 않아 다음에 추가 포스팅하는 걸로 하겠다.(죄송합니다.)
- 정의
검색을 해보면, 라디안에 대한 설명이 아주 잘 나와있고, 쉽게 찾아볼 수 있다. 우리 친구 위키피디아의 설명에 따라 정의를 알아보자.


정리한 대로 이야기해보자면,
반지름이 r이라고 했을 때, 호의 길이가 반지름과 같은 r이라면, 그때의 호의 각도를 1 라디안이라고 한다.
그럼, 전체 원의 둘레를 기준을 한 원은 2π라디안이 되고, 결국 360˚ = 2π라디안이 된다.
그래서 라디안이 호의 길이에 따라 각도를 나타내기에 호도법이라고 지칭하기도 한다.
라디안과 각도가 서로 상응? 하여 비례식이 적용 가능하다. 그런 맥락에서 바라보면
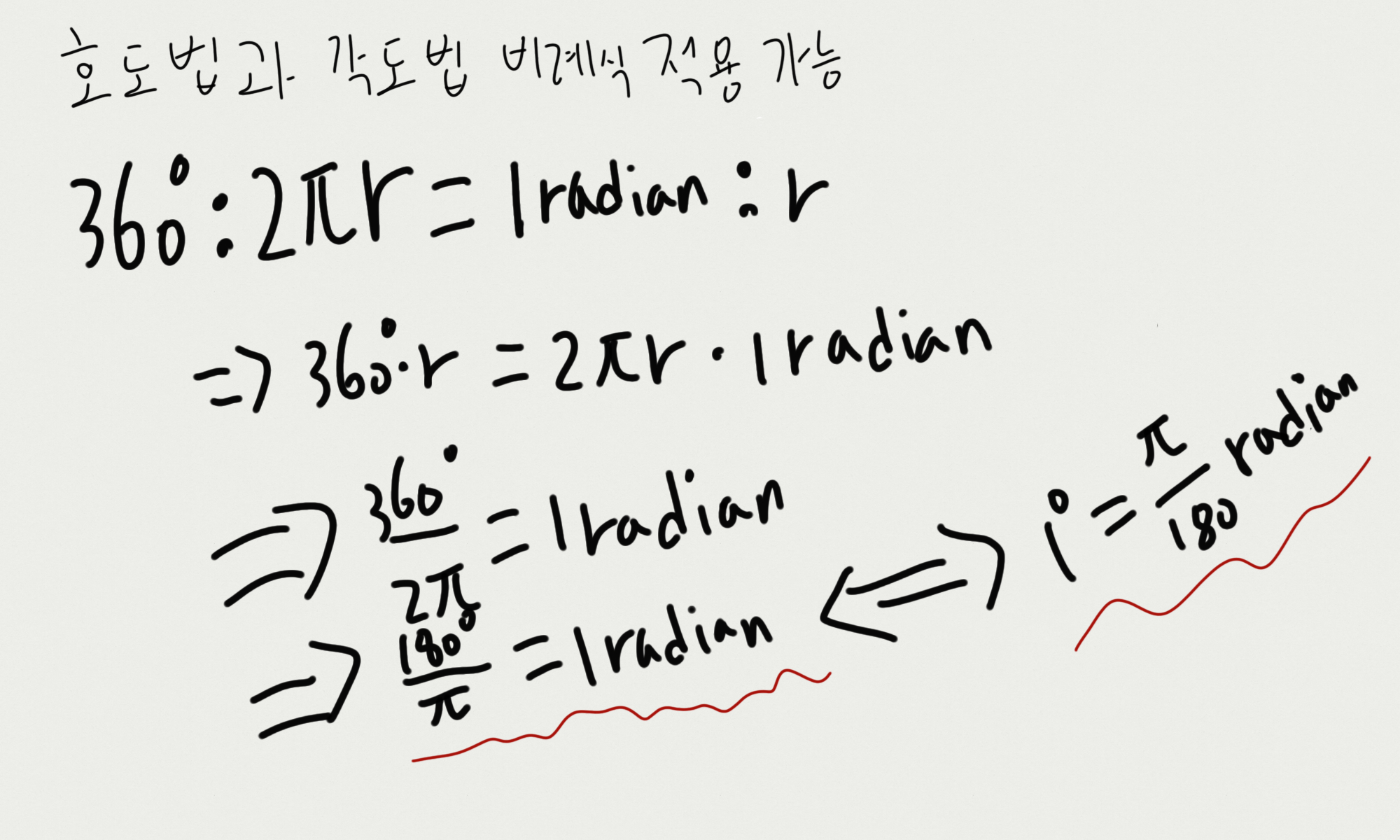
위의 그림과 같이 정리할 수 있다.
그렇기에 우리가 중고등학교? 에서 보던 아래의 표가 성립할 수 있는 것이다.
| 라디안 | 각도 |
| 0 | 0° |
| π/12 | 15° |
| π/6 | 30° |
| π/5 | 36° |
| π/4 | 45° |
| π/3 | 60° |
| 2π/5 | 72° |
| π/2 | 90° |
| 2π/3 | 120° |
| 4π/5 | 144° |
| π | 180° |
| 3π/2 | 270° |
| 2π | 360° |
* 참조
- https://ko.wikipedia.org/wiki/%EB%9D%BC%EB%94%94%EC%95%88
라디안 - 위키백과, 우리 모두의 백과사전
라디안단위의 종류SI 유도 단위측정 대상각기호rad 또는 c 단위무한분량단위 환산 1 rad ▼동등 환산값 밀리라디안 1,000 밀리라디안 바퀴 1/2π 바퀴 도 180/π ≈ 57.296°
ko.wikipedia.org
'머신러닝 > 수학' 카테고리의 다른 글
| [수학] 쌍곡선함수, 쌍곡삼각함수 / hyperbolic function, sinh, cosh, tanh (0) | 2021.10.10 |
|---|---|
| [수학] 삼각함수의 기본 - sin cos tan의 정의와 주기/ 사인, 코사인, 탄젠트에 대한 간단한 정리 (0) | 2021.10.07 |
| [수학] 정규분포란 (0) | 2021.09.28 |
| [수학] 용어정리 (0) | 2021.09.18 |
| [수학] 내가 왜 이런거까지?2 항등원, 역원 (0) | 2021.09.18 |



댓글