오늘도 전처리 과정의 일환이다. Numpy는 머신러닝, 딥러닝에 활용된다. 앞선 포스팅 내용들을 통해 전처리과정을 거친 후에도 결국 일정한 수치, 데이터를 만들어 수학적 계산을 진행해야 한다. 그 계산들은 다양한 방식으로 진행돼야 한다.
간단하게는 행, 열을 기준으로 총합, 평균을 구하는 경우가 상황에 따라 존재할 수 있다.
그런 계산의 기준을 Numpy에선 "axis(축)"으로 표현한다.
- np.sum() 총합
import numpy as np
a = np.arange(3*3).reshape((3, 3))
print(a)
# [[0 1 2]
# [3 4 5]
# [6 7 8]]
sum_ = a.sum()
sum_axis_0 = a.sum(axis=0)
sum_axis_1 = a.sum(axis=1)
print(sum_) # 36
print(sum_axis_0) # [ 9 12 15]
print(sum_axis_1) # [ 3 12 21]위의 코드에 대한 이해를 그림으로 정리해보았다

- axis(축)을 기준으로 계산을 한다. 축을 기준을 한다는 것이 즉각적으로 이해되지 않으면, 기준 축이 사라진다고 이해해보자. 기준 축이 사라지고, 그 축끼리 연산이 이루어진다고 이해하자.
import numpy as np
a = np.arange(2*3*4).reshape((2,3,4))
print(a)
# [[[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]
sum_ = a.sum()
sum_axis_0 = a.sum(axis=0)
sum_axis_1 = a.sum(axis=1)
sum_axis_2 = a.sum(axis=2)
print(sum_) # 276
print(sum_axis_0)
# [[12 14 16 18]
# [20 22 24 26]
# [28 30 32 34]]
print(sum_axis_1)
# [[12 15 18 21]
# [48 51 54 57]]
print(sum_axis_2)
# [[ 6 22 38]
# [54 70 86]]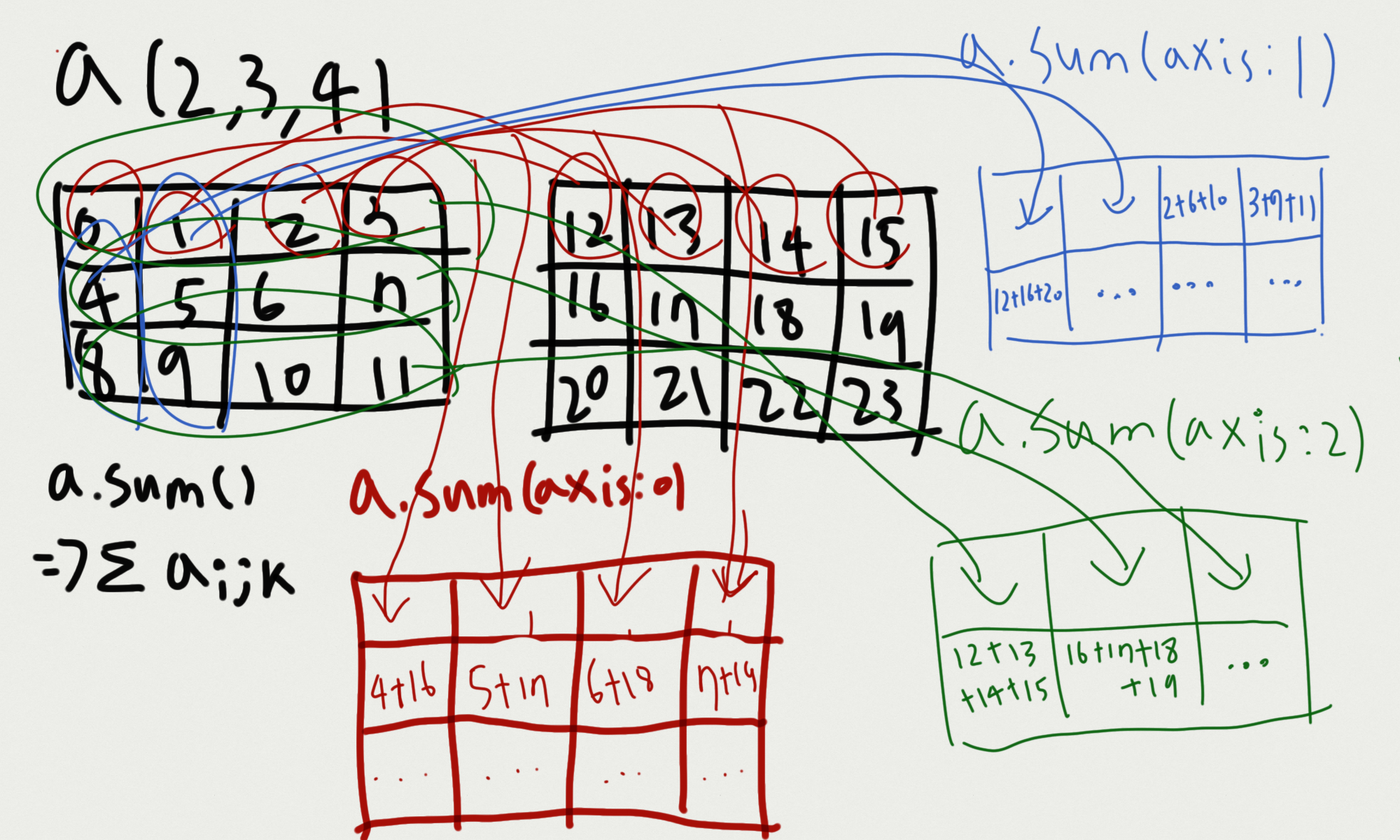
그림이 복잡해 보이긴 하지만, 다차원 배열 역시 축으로 한 기준 그리고, 해당 차원끼리의 계산을 하고, 해당 차원이 사라진다는 개념으로 이해하고 바라보자.
- 과목별 점수 합계, 학생별 점수 합계
학생 5명의 3개의 과목(국영수)에 대한 점수 데이터가 있다.
과목별 점수 합계, 학생별 점수 합계를 구해보자
import numpy as np
scores = np.random.randint(0, 101, (5, 3))
print(scores)
# [[ 90 59 100]
# [ 87 86 73]
# [ 78 86 34]
# [ 49 4 14]
# [ 18 95 74]]
scores_class = np.sum(scores, axis=0)
print(scores_class) # [322 330 295]
scores_student = np.sum(scores, axis=1)
print(scores_student) # [249 246 198 67 187]
다시 한번 그림이 어지럽지만, 위 그림과 같이 계산이 된다. 실제 데이터들은 각각의 행과 열이 의미를 가지고 있다. 전처리 과정에서 reshape 등으로 계산이 간편하게 만들겠지만, 결국 축을 기준으로 한 계산은 필요하다.
- np.mean() 평균
import numpy as np
a = np.arange(3*3).reshape((3, 3))
print(a)
# [[0 1 2]
# [3 4 5]
# [6 7 8]]
mean_ = a.mean() # 4.0
mean_axis_0 = a.mean(axis=0)
mean_axis_1 = a.mean(axis=1)
print(mean_) # 36
print(mean_axis_0) # [3. 4. 5.]
print(mean_axis_1) # [1. 4. 7.]평균 역시 위의 np.sum()과 같이 동일하게 진행된다.

import numpy as np
a = np.arange(2*3*4).reshape((2,3,4))
print(a)
# [[[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]
mean_ = a.mean()
mean_axis_0 = a.mean(axis=0)
mean_axis_1 = a.mean(axis=1)
mean_axis_2 = a.mean(axis=2)
print(mean_) # 11.5
print(mean_axis_0)
# [[ 6. 7. 8. 9.]
# [10. 11. 12. 13.]
# [14. 15. 16. 17.]]
print(mean_axis_1)
# [[ 4. 5. 6. 7.]
# [16. 17. 18. 19.]]
print(mean_axis_2)
# [ 1.5 5.5 9.5]
# [13.5 17.5 21.5]]
반복이지만, 기준을 중심으로 계산! 그렇기에 기준이 사라진다고 생각하자
- 과목별 점수 평균, 학생별 점수 평균
학생 5명의 3개의 과목(국영수)에 대한 점수 데이터가 있다.
과목별 점수 평균 학생별 점수 평균을 구해보자
import numpy as np
scores = np.random.randint(0, 101, (5, 3))
print(scores)
# [[46 11 79]
# [84 75 95]
# [61 52 34]
# [24 28 60]
# [68 35 5]]
scores_class = np.mean(scores, axis=0)
print(scores_class) # [56.6 40.2 54.6]
scores_student = np.mean(scores, axis=1)
print(scores_student)
# [45.33333333 84.66666667 49. 37.33333333 36. ]그림으로 설명해보자면
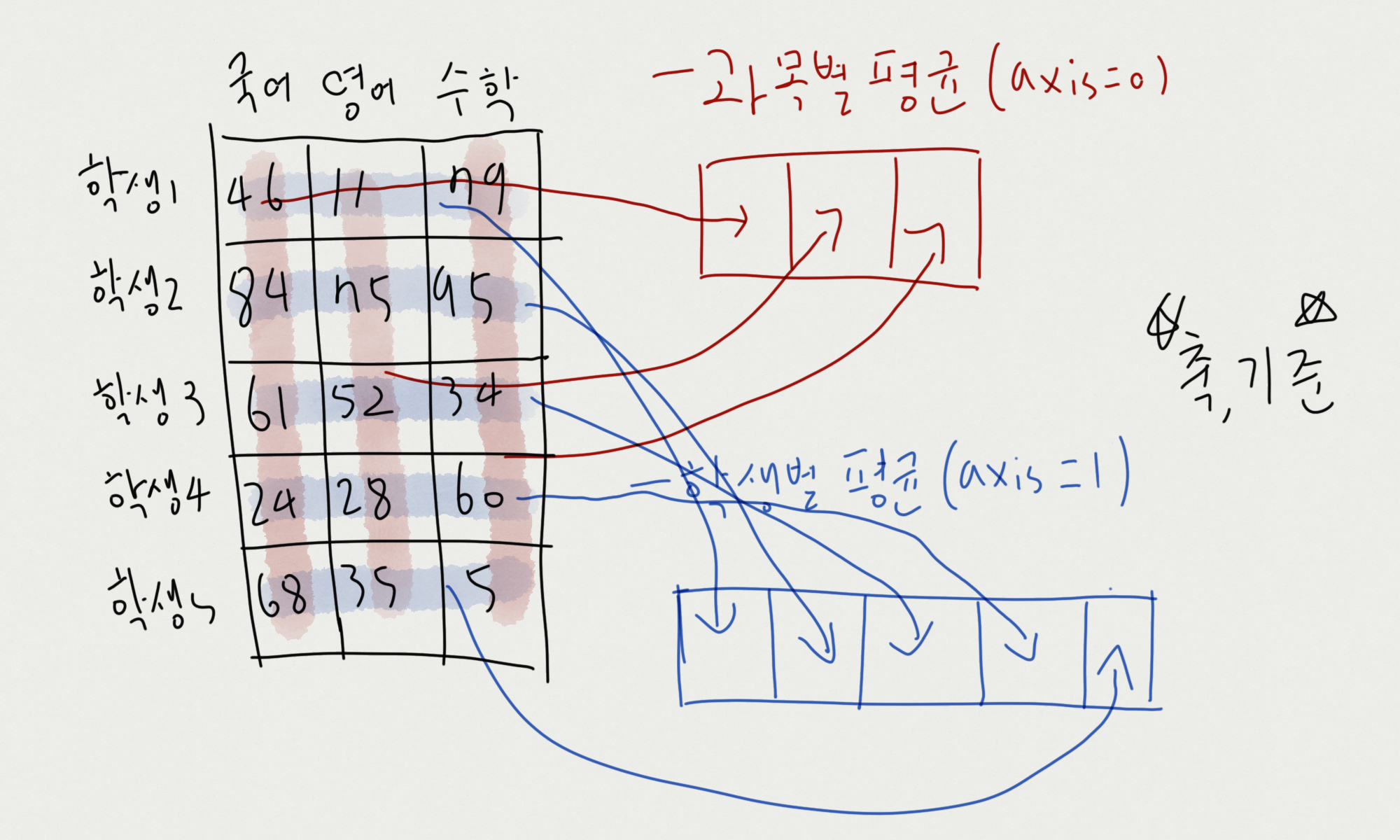
위와 같은 그림으로 계산된다. 축, 기준을 항상 명심하자.
- keepdims
그런데 위의 예제에서 학생별 평균, 합계를 구할 때 조금 불편한 것을 못 느꼈나? 왜 그림을 기준으로 보자면 세로끼리 연산을 했는데 왜 결과는 가로의 형태로 나온 것일까? 이런 방식이 연산에 불편함을 줄 수도 있지 않을까?
실제 가정
- 시험 문제가 잘못돼 학생들에게 점수로 보상을 해줘야 할 경우, 본인들의 평균의 15%씩을 추가로 더해주겠다고 가정을 해보자.
import numpy as np
scores = np.random.randint(0, 101, (5, 3))
print(scores)
# [[10 57 75]
# [18 55 99]
# [63 47 39]
# [14 25 24]
# [13 91 66]]
# 학생 평균
scores_student = np.mean(scores, axis=1)
print(scores_student)
# [47.33333333 57.33333333 49.66666667 21. 56.66666667]
# print(scores + (scores_student * 0.15)) # broadcast error
print(scores.shape, (scores_student * 0.15).shape) # (5, 3) (5,)당장 머릿속으로 생각한 그림을 코드로 짜보면, scores + (scores_student * 0.15)의 형태로 연산을 진행하면 좋겠다고 생각했지만, broadcast error가 발생한다. 당연하다! (5, 3)와 (5, )은 broadcasting이 불가능하니까..
이럴 때, 활용 가능한 것이 "keepdims"이다.
keepdims는 "keep dimensions"으로, 말 그대로 "차원을 유지한다"는 의미의 속성이다.
이 keepdims를 활용해보면!
import numpy as np
scores = np.random.randint(0, 101, (5, 3))
print(scores)
# [[24 72 71]
# [ 5 19 35]
# [80 12 4]
# [66 71 85]
# [55 60 34]]
# 학생 평균
scores_student = np.mean(scores, axis=1, keepdims=True) # keepdims=True 추가
print(scores_student)
# [[55.66666667]
# [19.66666667]
# [32. ]
# [74. ]
# [49.66666667]]
print(scores.shape, (scores_student * 0.15).shape) # (5, 3) (5, 1)
print(scores + (scores_student * 0.15))
# [[32.35 80.35 79.35]
# [ 7.95 21.95 37.95]
# [84.8 16.8 8.8 ]
# [77.1 82.1 96.1 ]
# [62.45 67.45 41.45]]keepdims=True를 추가하니 (scores_student * 0.15)의 shape이 (5, 1)이 됐다. 그렇게 되면, broadcasting이 일어나 연산이 가능하게 된다.

위의 그림과 같이 진행된다.
import numpy as np
scores = np.random.randint(0, 101, (5, 3))
# 학생 평균
scores_student = np.mean(scores, axis=1, keepdims=True)
print(scores_student.shape) # (5, 1)
# 과목 평균
scores_class = np.mean(scores, axis=0, keepdims=True)
print(scores_class.shape) # (1, 3)위에서 axis(축)을 설정하게 되면, 그 축을 기준으로 연산을 하기에 축이 사라진다고 설명했다.
좀 더 깊게 바라보면 축을 기준으로 행은 행끼리, 열은 열끼리 연산을 해 사실은 "하나의 값, 데이터"가 된다.
keepdims는 그 하나를 유지한다는 의미의 속성이다.
오늘은 np.sum(), np.mean(), axis, keepdims 등 "axis(축)"을 기준으로 한 연산과 그와 관련한 속성에 대해 알아보았다.
다음 포스팅은 이를 바탕으로 한 좀 더 복잡한 연산에 대해 알아보겠다.


댓글