
우리가 이번 포스팅을 통해 이끌어내고 싶은 결과물이다.
왼쪽에서부터 "원본사진", "rgd(255,0,0)=Red", "rgd(0,255,0)=Green", "rgd(0,0,255)=Blue"와 닮은 색상 추출
- 포스팅의 목적 : 이미지에서 특정 rgb의 값과 닮은 색상 추출
이 결과물을 이미지를 분석한 후, 코사인 유사도를 통해 유도해보겠다.
이 과정을 위해 우리는 이론적 정리가 필요하다.
1. 이미지 분석

원본이 w,h 크기가 같아 크기를 조정했습니다
import numpy as np
from matplotlib import pyplot as plt
img = plt.imread('test_image.jpg')
print(img.shape) # (350, 500, 3)해당 이미지를 읽어 들여서 shape을 확인해보면, 위의 코드와 같이 (350, 500, 3)으로 확인할 수 있다.

이미지 정보를 확인해보면
(350, 500, 3)은 (height, width, rgb정보 값)이라는 것을 알 수 있겠다.
그러면, numpy 문법을 활용해보면
import numpy as np
from matplotlib import pyplot as plt
img = plt.imread('test_image.jpg')
print(img.shape) # (350, 500, 3) = (height(세로), width(가로), rgb정보값)
img_indies = [*img.shape] # unpacking
height_half = int(img_indies[0]/2)
width_half = int(img_indies[1]/2)
left_top = img[:height_half, :width_half]
right_top = img[:height_half, width_half:]
left_bottom = img[height_half:, :width_half]
right_bottom = img[height_half:, width_half:]
fig, axes = plt.subplots(2, 2, figsize=(30, 15))
axes[0, 0].imshow(left_top)
axes[0, 1].imshow(right_top)
axes[1, 0].imshow(left_bottom)
axes[1, 1].imshow(right_bottom)
plt.show()
위의 코드와 같이 3차원배열에서 각 차원들의 의미를 이해하면, 이런 식으로 이미지를 원하는 방식으로 나타낼 수도 있다.
다시 정리하면, "jpg" 이미지파일은 (height, width, rgb정보 값)의 모양으로 나타낼 수 있다.
예를 들어,
import numpy as np
from matplotlib import pyplot as plt
img = plt.imread('test_image.jpg')
print(img[150][230][0]) # 209
print(img[150][230][1]) # 152
print(img[150][230][2]) # 123이런 식의 코드가 있다고 하면,
- img[150][230][0] : height(위에서부터) 150번째, width(왼쪽에서부터) 230번째 픽셀의 rgb 중 r의 값 209
- img[150][230][1] : height(위에서부터) 150번째, width(왼쪽에서부터) 230번째 픽셀의 rgb 중 g의 값 152
- img[150][230][2] : height(위에서부터) 150번째, width(왼쪽에서부터) 230번째 픽셀의 rgb 중 b의 값 123

해당 픽셀의 rgb값은 이런 색이구나!라는 식의 분석이 가능하다.
이렇게 픽셀 하나하나의 rgb값이 모여 이미지가 되는 것이다.
- 이미지 파일을 이와 같은 데이터 값을 갖는다. 이 데이터를 어떠한 방식으로 처리해서 원하는 결과물을 얻을까? 관련해서 알아야 할 이론적 내용들이 있다.
2. Dot Product
- Dot Product에 대한 정의는 "스칼라곱(scalar product) 또는 점곱(dot product)은 유클리드 공간의 두 벡터로부터 실수 스칼라를 얻는 연산이다. 스칼라곱이 유클리드 공간의 내적을 이루므로, 이를 단순히 '내적'이라고 부르기도 한다. 스칼라곱의 개념의 물리학 배경은 주어진 힘이 주어진 변위의 물체에 가한 일을 구하는 문제이다." 이와 같다.
2-1. 대수학에서의 Dot Product와 계산과정
- Dot Product는 아래와 같이 표현된다.
$$ a \cdot b $$
- Dot Product는 아래와 같이 계산된다.
$$ a \cdot b = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 + \ldots + a_n b_n$$
- 또한 벡터들을 행렬로 바라볼 경우
$$ a \cdot b = a^T b $$
위와 같이 표현될 수 있는데, 여기서 T는 tranpose로 (행 행렬 -> 열 행렬), (열 행렬 -> 행 행렬)로 변환한다는 의미의 기호이다.
그리고 해당 표현은 행렬 상에서
$$\begin{pmatrix}1&2&3\end{pmatrix}\begin{pmatrix}4\\5\\6\\\end{pmatrix} = \begin{pmatrix}1\cdot4&2\cdot5&3\cdot6\end{pmatrix} = 32\;(=1\cdot4+2\cdot5+3\cdot6) $$
이와 같이 처리된다.
2-2. 기하학에서의 Dot Product와 의미
- 기하학에서 Dot Product는 아래와 같이 정의된다.
$$ a \cdot b = \begin{Vmatrix} a \end{Vmatrix} \begin{Vmatrix} b \end{Vmatrix} \cos \theta$$
위의 정의에서
- ||a|| : a의 길이
- ||b|| : b의 길이
- θ : a와 b 사이의 각도
> 기하학에의 Dot Product(내적) = a의 길이 * b의 길이 * cosθ

위와 같은 그림으로 표현된다.
- 기하학에서의 특별한 예
1. a · a
- θ : 0˚
- a · a = |a||a|cos0 > cos0 = 1
- a · a = |a|²
2. a와 b의 각도가 90˚일 때
- θ : 90˚
- a · b = |a||b|cos90 (cos90 = 0)
- a · b = 0
- 추가적으로 코사인 법칙 등으로 내적 증명하는 과정이 있으나, 아직 이해도가 부족해 추가적인 공부 이후에, 포스팅하겠음
3. Vector Norm
- Norm은 Vector의 크기 및 길이를 측정할 때 사용하는 방법, 개념이다
$$ \begin{Vmatrix} X \end{Vmatrix}_{p} := \left(\sum_{i=1}^n \left| x_{i} \right|^p \right)^{\frac{ 1 }{ p }} $$
- 위와 같이 정의되고, 실제로 자주 활용되는 경우는 p=1, p=2일 경우이다. 우리는 p=1일 경우를 L1 Norm(Manhattan norm, Taxicab norm)이라고 부르고, p=2일 경우를 L2 Norm(Euclidean Norm)이라 부릅니다.
3-1. L1 Norm
$$ \begin{Vmatrix} X \end{Vmatrix}_{1} := \left(\sum_{i=1}^n \left| x_{i} \right|^1\right)^{\frac{ 1 }{ 1 }} = \left(\sum_{i=1}^n \left| x_{i} \right| \right)$$
- 요소들의 절댓값의 합
- Manhattan norm, Taxicab norm
예시
- 나와 친구가 3차원 그래프(x, y, z)상에 있다. 나는 친구를 만나러 가기로 약속을 했고, 친구가 자신의 좌표를 알려주었다. 나는 직선(1차원의 이동) 이동만 할 수 있을 때, 내가 친구에게까지 가는데, 걸리는 최소 이동거리는?
- 친구의 좌표 : (130, 250, 85),
나의 좌표 : (100, 75, 180),
친구 좌표 - 내 좌표 : (130-100, 250-75, 85-180) = (30, 175, -95),
차원마다의 이동거리 : (30, 175, 95)
총 이동거리 : (30 + 175 + 95) = 300
위와 같은 문제가 있을 때, L1 Norm을 활용할 수 있다
import numpy as np
friend_xyz = np.array([130, 250, 85])
my_xyz = np.array([100, 75, 180])
# 친구좌표 - 내좌표
friend_sub_i = friend_xyz - my_xyz
print(friend_sub_i) # [30 175 -95]
# 절대값
abs = np.abs(friend_sub_i)
print(abs) # [30 175 95]
# 총이동거리
distance = np.sum(abs)
print(f"총이동거리 : {distance}") # 총이동거리 : 300
3-2. L2 Norm
$$ \begin{Vmatrix} X \end{Vmatrix}_{2} := \left(\sum_{i=1}^n \left| x_{i} \right|^2\right)^{\frac{ 1 }{ 2 }} = \sqrt{\sum_{i=1}^n \left| x_{i} \right|^2 } $$
- 모든 요소들의 제곱의 합의 제곱근
- Euclidean Norm
- 어디서 본 적 있지 않은가?


피타고라스의 정리는 왼쪽의 그림과 같이 다차원의 경우에도 동일하게 적용된다.
$$ A^2_{ABC} = A^2_{ABO} + A^2_{BCO} + A^2_{CAO} $$
$$ A_{ABC} = \sqrt{A^2_{ABO} + A^2_{BCO} + A^2_{CAO}} $$
예시
- 나와 친구가 3차원 그래프(x, y, z)상에 있다. 나는 친구를 만나러 가기로 약속을 했고, 친구가 자신의 좌표를 알려주었다. 나는 평면상의 이동(2차원의 이동)을 할 수 있을 때, 내가 친구에게까지 가는데, 걸리는 최소 이동거리는?
- 친구의 좌표 : (130, 250, 85),
나의 좌표 : (100, 75, 180),
친구 좌표 - 내 좌표 : (130-100, 250-75, 85-180) = (30, 175, -95),
import numpy as np
friend_xyz = np.array([130, 250, 85])
my_xyz = np.array([100, 75, 180])
# 친구좌표 - 내좌표
friend_sub_i = friend_xyz - my_xyz
print(friend_sub_i) # [30 175 -95]
# 제곱
square = np.square(friend_sub_i)
print(square) # [ 900 30625 9025]
# sum
sum = np.sum(square)
print(sum) # 40550
# 제급근
distance = np.sqrt(sum)
print(f"총이동거리 : {distance.round(2)}") # 총이동거리 : 201.371차원 이동을 하다 2차원 이동을 하니 거리가 줄어들었네!
4. Unit Vector
- Unit Vector : 단위 벡터라고 부르며, 크기가 1인 벡터를 의미한다.
$$ 벡터\ v와\ 방향이\ 같은\ 단위벡터\ =\ \hat{v} \ , \ (v\ hat) $$
4-1. Unit Vector 구하기, Vector Unitization, 단위 벡터화
$$ \vec{a}의\ \hat{a}\ = \ \frac{1}{\left|\vec{a}\right|}\cdot\vec{a}$$
- Unit Vector 구하는 방법은 위의 수식과 같이 정의된다.
예제
- 벡터 a가 (3, 4)라고 했을 때의 단위 벡터를 구하시오

정리노트에 적은 것처럼, 단위 벡터는 벡터들의 크기와 방향을 나타내는데 효과적인 개념이다!
- Python code
import numpy as np
a = np.array([3, 4])
a_크기 = np.sqrt(np.sum(np.square(a))) # x, y 제곱 -> 모두 더하기 -> 더한 값 루트
print(a_크기) # 5.0
a_unit = a / a_크기
print(a_unit) # [0.6 0.8]
5. Cosine Similarity
- Cosine Similarity는 코사인 유사도라고 불리며, 내적 공간의 두 벡터 간 각도의 코사인 값을 이용하여 측정된 벡터 간의 유사한 정도를 의미한다.
- 각도에 따라
θ : 0˚ : cos0 = 1
θ : 90˚ : cos90 = 0
θ : 180˚ : cos180 = -1
으로 방향의 유사도를 판단할 수 있다
- cos값 유도(feat. wiki)
코사인 값은 유클리드 Dot Prudct 공식을 유도할 수 있다.
$$ a \cdot b = \begin{Vmatrix} a \end{Vmatrix} \begin{Vmatrix} b \end{Vmatrix} \cos \theta$$
$$ similarity(유사도)\ = \ cos(\theta)\ = \frac{A \cdot B}{\left| \left| A \right| \right| \left| \left| B \right| \right| } = \frac{\sum_{i=1}^n A_i \times B_i}{\sqrt{\sum_{i=1}^n (A_i)^2} \times \sqrt{\sum_{i=1}^n (B_i)^2}} $$
- 위의 수식을 보게 되면 cos값은 벡터끼리의 유클리드 Dot Product를 통해 유도할 수 있다.
- 그리고 cos값은 벡터끼리의 떨어져 있는 정도를 나타냄으로, 유사도를 알아낼 수 있다.
- 다양한 정의와 수식, 증명이 있지만, 포스팅의 목적을 달성시킬 최소한의 정리만 서술하도록 하겠다.
예제
- 나와 친구 A, B가 2차원 좌표계 위에 있다. 친구 A, B의 좌표를 통해 누가 나와 더 가까운지 알아보도록 하자. 코사인 유사도 사용
나의 좌표 : (3, 4)
친구 A의 좌표 : (10, 27)
친구 B의 좌표 : (35, 7)
import numpy as np
my_xy = np.array([3, 4])
friend_a_xy = np.array([10, 27])
friend_b_xy = np.array([35, 7])
# 나와 친구 a의 cosine similarity
my_norm = np.sqrt(np.sum(np.square(my_xy)))
a_norm = np.sqrt(np.sum(np.square(friend_a_xy)))
a_similarity = np.sum(my_xy * friend_a_xy) / (my_norm * a_norm)
print(a_similarity) # 0.9585876220731193
# 나와 친구 b의 cosine similarity
my_norm = np.sqrt(np.sum(np.square(my_xy)))
b_norm = np.sqrt(np.sum(np.square(friend_b_xy)))
b_similarity = np.sum(my_xy * friend_b_xy) / (my_norm * b_norm)
print(b_similarity) # 0.7452413135250993print(a_similarity) # 0.9585876220731193
print(b_similarity) # 0.7452413135250993코드를 통해 확인해보면, a와의 유사도가 더 1에 가까움으로 나와는 친구 a가 더 가깝다는 것을 알 수 있다.
실제로 그러한지 확인해 보록 하자
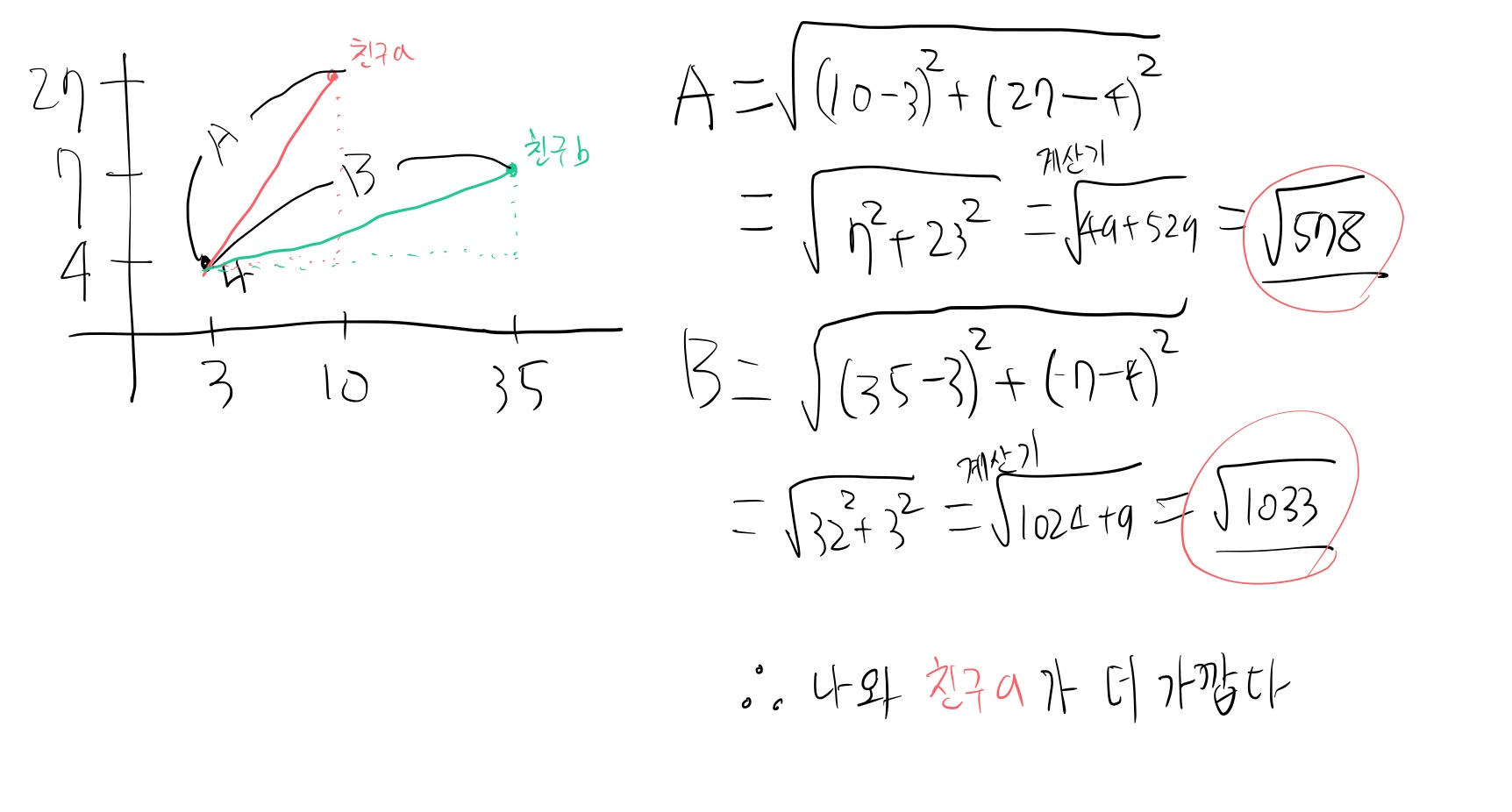
- 유클리드 거리 법(aka. 소크라테스 따라쟁이)을 사용해 확인해보니(그냥 코드로 해도 됐잖아..) 친구 a가 더 가깝다는 걸 확인할 수 있었다.
- 그렇다면, 유클리드 거리 법으로도 거리 및 차이를 확인할 수 있음에도 불구하고, 왜 코사인 유도법을 사용하는 걸까?
간략하게 요약하자면, 코사인 유도법은 "방향"에 집중하기 때문이다. 유사한 것들끼리 거리가 멀 수도 있고, 유사하지 않을 것들끼리 거리가 가까울 수 있는 경우가 존재함.
* 관련 설명 https://www.youtube.com/watch?v=EGEQutnxjDU&t=341s
- 이렇게 해서 포스팅의 목적인 "코사인 유도를 통한 색 추출"을 위한 이론 공부 및 설명이 끝났다. 이론 공부를 하며, 내 수학적 지식이 정말 부족하다는 것을 느꼈다. 특히, 전공자들이 봤을 때, 틀리거나 불명확한 설명이 있을 것이다. 앞으로 계속 배워나가며 차근차근 수정하고 새로운 포스팅으로 채워나가겠다.
6. Cosine Similarity를 통한 Color extraction

import numpy as np
from matplotlib import pyplot as plt
img = plt.imread('test_rgb.jpg')
print(img.shape, img.dtype)
img_norm = np.sqrt(img[..., 0]**2 + img[..., 1]**2 + img[..., 2]**2)
img_norm = np.reshape(img_norm, (img_norm.shape + (1, )))
img_unit = img / img_norm
R, G, B = [255.0, 0., 0.], [0., 255., 0.], [0., 0., 255.]
t_r = np.array(R)
t_r_norm = np.sqrt(np.sum(t_r**2))
t_r_unit = t_r / t_r_norm
img_dot_r = np.sum(img_unit * t_r_unit, axis=-1)
t_g = np.array(G)
t_g_norm = np.sqrt(np.sum(t_g**2))
t_g_unit = t_g / t_g_norm
img_dot_g = np.sum(img_unit * t_g_unit, axis=-1)
t_b = np.array(B)
t_b_norm = np.sqrt(np.sum(t_b**2))
t_b_unit = t_b / t_b_norm
img_dot_b = np.sum(img_unit * t_b_unit, axis=-1)
fig, axes = plt.subplots(1, 4, figsize=(30, 10))
axes[0].imshow(img.astype(np.uint8))
axes[1].imshow(img_dot_r, cmap="gray")
axes[2].imshow(img_dot_g, cmap="gray")
axes[3].imshow(img_dot_b, cmap="gray")
fig.tight_layout()
plt.show()결과물과 해당 코드이다. 결과물을 어떻게 얻었는지 천천히 살펴보도록 하겠다.
6.1 이미지 분석

img = plt.imread('test_rgb.jpg')
print(img.shape, img.dtype) # (500, 500, 3) uint8위의 이미지는
- height : 500, width :500, rgb의 값 / uint8 타입
으로 구성되어있다.

간략하게 보면, 위의 그림과 같이 구성돼있다.
6.2 rgb의 norm, unit vector 구하기
img_norm = np.sqrt(img[..., 0]**2 + img[..., 1]**2 + img[..., 2]**2)
img_norm = np.reshape(img_norm, (img_norm.shape + (1, )))
img_unit = img / img_norm- 첫 번째 코드
각각의 좌표들의 rgb값을 하나의 벡터로 보고, L2 norm 방식을 통해 norm(벡터의 크기)을 구하는 코드이다.
$$ \sqrt{\sum_{i=1}^n \left| x_{i} \right|^2 } \rightarrow \sqrt{ r^2 + g^2 + b^2 } $$
- 두 번째 코드
img_norm = np.sqrt(img[..., 0]**2 + img[..., 1]**2 + img[..., 2]**2)
print(img_norm.shape) # (500, 500)첫 번째 코드가 진행되면 img_norm의 shape은 위 코드와 같이 (500, 500)으로 변경된다.
이 상태에서는 img(shape=(500,500,3))과 연산할 수 없기 때문에 모양을 바꿔 주는 것이다.
img_norm = np.sqrt(img[..., 0]**2 + img[..., 1]**2 + img[..., 2]**2)
print(img_norm.shape) # (500, 500)
img_norm = np.reshape(img_norm, (img_norm.shape + (1, )))
print(img_norm.shape) # (500, 500, 1)두 번째 코드까지 진행되면 img_norm의 shape은 (500, 500, 1)로 img와 연산이 가능한 상태가 된다.
- 세 번째 코드
단위 벡터를 구하는 코드이다. 단위 벡터는 위에서 서술했듯이, "벡터/벡터의 크기"이다.
단위 벡터를 구함으로써 벡터들의 방향을 파악할 수 있다.
지금까지 살펴본 내용을 그림으로 그려보자면

> 이미지의 임의의 pixel (H, W)
> (H, W)의 RGB 값을 "(r, g, b)"이고, 우리는 색 분석 및 추출의 할 것이니, (r, g, b)를 벡터로 보겠다.
> 이후 rgb값을 통해 norm을 구하고, 단위 벡터까지 구해보았다.
6.3 target rgb의 unit vector 구하기, target rgb와의 유사도 구하기
R, G, B = [255., 0., 0.], [0., 255., 0.], [0., 0., 255.]
t_r = np.array(R)
t_r_norm = np.sqrt(np.sum(t_r**2))
t_r_unit = t_r / t_r_norm
img_dot_r = np.sum(img_unit * t_r_unit, axis=-1)
...
# 아래 코드 동작은 위의 코드 동작과 동일하게 생략하겠다.
- 첫 번째 코드
원본 이미지와 비교할 색상을 정해주었다. [255, 0, 0](R, 빨간색) / [0, 255, 0](G, 초록색) / [0, 0, 255](B, 파란색)
- 두 번째 코드
t_r = np.array(R) # (3, )numpy 연산을 위한 ndarray화
- 세 번째 코드
t_r_norm = np.sqrt(np.sum(t_r**2)) # 255.0L2 norm 방식을 통해, rgb값의 norm을 구한다
- 네 번째 코드
t_r_unit = t_r / t_r_norm # [1. 0. 0.]norm을 통해 단위 벡터를 구한다
- 다섯 번째 코드
계산하기 전에 img_unit과 t_r_unit의 shape를 살펴보면
print(img_unit.shape, t_r_unit.shape) # (500, 500, 3) (3,)이러한 shape일 때
img_unit * t_r_unit위 코드의 연산이 이루어지면

위의 그림에서 설명하듯, img_unit은 "이미지 pixel들의 RGB 값들의 유닛 벡터"이고,
t_r_unit은 우리가 target으로 설정한 RGB(255,0,0)의 유닛 벡터이다.
이 둘이 (500, 500, 3), (3, )의 모양에서 곱셈 연산을 하게 되면,
브로드캐스팅이 일어나 (500, 500, 3) * (500, 500, 3)인 모양으로 연산이 진행된다.
(500, 500, 3) * (500, 500, 3) 연산이 일어나면,
img_r_u : image pixel의 R값의 유닛 벡터
img_g_u : image pixel의 G값의 유닛 벡터
img_b_u : image pixel의 B값의 유닛 벡터
target_r_u : target RGB 중 R값의 유닛 벡터
target_g_u : target RGB 중 G값의 유닛 벡터
target_b_u : target RGB 중 B값의 유닛 벡터
(img_r_u * target_r_u , img_g_u * target_g_u, img_b_u * target_b_u)
위와 같은 식으로 계산이 되고, shape은 (500, 500, 3)이 된다.
print((img_unit * t_r_unit).shape) # (500, 500, 3)그 이후 axis=-1(= (500, 500, 3) 중 맨 마지막 3을 기준으로) 전체 합을 진행하면
np.sum(img_unit * t_r_unit, axis=-1)
위에서 배운 내적, 내적의 연산이 진행된 셈이다.

pixel 각각의 rgb와 target으로 정한 rgb의 단위 벡터끼리 Dot Product 연산을 진행하였기에
target rgb를 기준으로 pixel 각각의 rgb가 얼마나 유사한가를 결과물로 갖게 된다.
6.4 최종 결과물 도출
이러한 과정을 통한 결과물을 보게 되면
import numpy as np
from matplotlib import pyplot as plt
img = plt.imread('test_rgb.jpg').astype(np.float64)
img_norm = np.sqrt(img[..., 0]**2 + img[..., 1]**2 + img[..., 2]**2)
img_norm = np.reshape(img_norm, (img_norm.shape + (1, )))
img_unit = img / img_norm
R, G, B = [255.0, 0., 0.], [0., 255., 0.], [0., 0., 255.]
t_r = np.array(R)
t_r_norm = np.sqrt(np.sum(t_r**2))
t_r_unit = t_r / t_r_norm
img_dot_r = np.sum(img_unit * t_r_unit, axis=-1)
fig, axes = plt.subplots(1, 2, figsize=(30, 10))
axes[0].imshow(img.astype(np.uint8))
axes[1].imshow(img_dot_r, cmap="gray")
fig.tight_layout()
plt.show()
> target rgb가 (255, 0, 0)이었기에
> 빨간색 원에 가까울수록 img_dot_r의 값이 커지게 되고, rgb의 값이 커지다는 것은 흰색에 가까워짐을 의미한다.
> 빨간색 원을 기준으로 빨간색이 많이 함유된 부분들은 밝게, 나머지는 어둡게 나오게 된다.
R, G, B = [255.0, 0., 0.], [0., 255., 0.], [0., 0., 255.]target rgb가 G, B도 있으니 R, G, B 모두 연산을 진행해보면,
import numpy as np
from matplotlib import pyplot as plt
img = plt.imread('test_rgb.jpg').astype(np.float64)
img_norm = np.sqrt(img[..., 0]**2 + img[..., 1]**2 + img[..., 2]**2)
img_norm = np.reshape(img_norm, (img_norm.shape + (1, )))
img_unit = img / img_norm
R, G, B = [255.0, 0., 0.], [0., 255., 0.], [0., 0., 255.]
t_r = np.array(R)
t_r_norm = np.sqrt(np.sum(t_r**2))
t_r_unit = t_r / t_r_norm
img_dot_r = np.sum(img_unit * t_r_unit, axis=-1)
t_g = np.array(G)
t_g_norm = np.sqrt(np.sum(t_g**2))
t_g_unit = t_g / t_g_norm
img_dot_g = np.sum(img_unit * t_g_unit, axis=-1)
t_b = np.array(B)
t_b_norm = np.sqrt(np.sum(t_b**2))
t_b_unit = t_b / t_b_norm
img_dot_b = np.sum(img_unit * t_b_unit, axis=-1)
fig, axes = plt.subplots(1, 4, figsize=(30, 10))
axes[0].imshow(img.astype(np.uint8))
axes[1].imshow(img_dot_r, cmap="gray")
axes[2].imshow(img_dot_g, cmap="gray")
axes[3].imshow(img_dot_b, cmap="gray")
fig.tight_layout()
plt.show()
우리가 포스팅 시작에서 목적으로 정했던 결과를 얻을 수 있게 된다!
7. 소감
다른 사람들이 보면 당연히 부족한 포스팅이겠지만, 나 스스로는 굉장히 뿌듯한 작업이었다. 프로젝트 목표를 잡고, 코사인 법칙도 모르는 내가 수학적 개념들을 하나하나 이해하고, 이해한 내용들을 적어 내려 가면서 프로젝트 목표와 점점 가까워질 수 있었다. 포스팅 시작 때는 정확히 이해하지 못했던 코드들도 이론들을 배우고 나니, 내용들을 좀 더 깊게 파악하고, 내가 파악 내용을 조금이나마 노트로 정리해 표현할 수 있게 되었다. 정말 의미 있는 프로젝트였고, 이러한 경험들이 차근차근 쌓여 좀 더 성장한 나를 만들길 바란다.
* 부족한 것들은 또또 포스팅하겠습니다. 보기에 미흡할 시 "그저 죄송"
* 참조
- https://ko.wikipedia.org/wiki/%EC%8A%A4%EC%B9%BC%EB%9D%BC%EA%B3%B1
스칼라곱 - 위키백과, 우리 모두의 백과사전
이 문서는 유클리드 공간 위의 내적에 관한 것입니다. 벡터 공간 위의 내적에 대해서는 내적 공간 문서를, 벡터와 스칼라의 곱셈에 대해서는 스칼라 곱셈 문서를 참고하십시오. 선형대수학에서,
ko.wikipedia.org
- http://www.mit.edu/~hlb/StantonGrant/18.02/details/tex/lec1snip2-dotprod.pdf
- https://en.wikipedia.org/wiki/Norm_(mathematics)
Norm (mathematics) - Wikipedia
Length in a vector space In mathematics, a norm is a function from a real or complex vector space to the nonnegative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequal
en.wikipedia.org
- https://ko.wikipedia.org/wiki/%EB%8B%A8%EC%9C%84%EB%B2%A1%ED%84%B0
단위벡터 - 위키백과, 우리 모두의 백과사전
선형대수학에서, 단위 벡터 (單位 vector, 영어: unit vector)는 길이가 '1'인 벡터를 뜻한다. 벡터 v {\displaystyle v} 와 방향이 같은 단위 벡터는 종종 알파벳 위에 곡절 부호 (circumflex) 를 쓰고, '햇'이라
ko.wikipedia.org
- https://youtube.com/watch?v=F4x2_HwYvVY&t=24s
- https://www.youtube.com/watch?v=OMf14JRf5v4
- https://ko.wikipedia.org/wiki/%EC%BD%94%EC%82%AC%EC%9D%B8_%EC%9C%A0%EC%82%AC%EB%8F%84
코사인 유사도 - 위키백과, 우리 모두의 백과사전
코사인 유사도(― 類似度, 영어: cosine similarity)는 내적공간의 두 벡터간 각도의 코사인값을 이용하여 측정된 벡터간의 유사한 정도를 의미한다. 각도가 0°일 때의 코사인값은 1이며, 다른 모든
ko.wikipedia.org
'머신러닝 > 미니프로젝트' 카테고리의 다른 글
| [미니프로젝트] 딥러닝에서 learning_rate(학습률)가 필요한 이유 (0) | 2021.10.21 |
|---|---|
| [미니프로젝트] 1 feature, 1 sample linear regression model 구현 (0) | 2021.10.20 |
| [미니프로젝트] Convolutional Layer, Conv2D, CNN, Image correlation (1) | 2021.10.17 |
| [미니프로젝트] Dense Layer에 대한 이해 / 뉴런, 퍼셉트론, 뉴런레이어, 다층 뉴런레이어, 뉴런네트워크 #딥러닝기초 (0) | 2021.10.12 |
| [미니프로젝트] KNN Classification, K-Means Clustering 이해 및 구현 (0) | 2021.10.08 |




댓글