[수학] 미분, 순간변화율, 도함수, 합성함수 미분에 대하여

딥러닝에서는 loss값을 통해 w(가중치), b(상수)를 업데이트합니다. 이 과정에서 "미분"개념이 활용됩니다. 

때문에 관련해서 미분에 대해 알아보려 한다.

 

목차

- 미분(with 위키피디아)

- 미분이란?

- 미분의 의미
- f(x)가 연속함수일 때의 변화율
- x₁ = x, x₂ = x+h일 때의 변화율 그리고 h가 0에 가까워질 때- 미분의 표기
- 미분 예제
- 미분의 법칙
- 합성함수의 미분

 

- 미분(with 위키피디아)

- 미분이란?

미분의 정의는 "어떤 함수의 정의역 속 각 점에서 함숫값의 변화량과 독립 변숫값의 변화량 비의 극한 혹은 극한들로 치역이 구성되는 새로운 함수"이다. 이 정의를 간단히 줄이면, 어떤 함수의 "미분계수", "순간 변화율"을 구하는 것이다. 이 정의 속에서 미분과 도함수는 같은 개념이다. 

 

어떤 함수의 한 점에서의 미분은 그 점에서의 접선의 기울기와 같다

 

- 미분의 의미

: 미분은 "비선형 함수"를 "선형 함수"로 "근사적"으로 나타내려는 시도이다. 

: 미분이 가능하지 않을 수도 있다(존재하지 않을 수도 있다). 미분이 모든 곳에서 존재하는 함수를 "미분 가능 함수"라고 한다. "미분 가능 함수"는 극한 "연속함수"이어야 한다. (연속함수이어도 연속 미분 가능 함수가 아닐 수 있음)

 

- f(x)가 연속함수일 때의 변화율

미분 개념을 이해하기 위해선 함수값이 x값에 따라 변화한다는 것을 이해하고, 그 함수값의 변화율을 이해해야 한다.

 

f(x)의 임의의 두 점의 함수값 변화율을 일반화해보면,

$$ 변화율 = \frac{f(x_2) - f(x_1)}{x_2 - x_1} $$

위 같은 수식이 나올 것이다.

 

"f(x) = 2x² + 3x + 5"을 예로 들어보자. x₁ = 3, x₂ = 5일 때의 변화율을 알아보자

$$ 변화율 = \frac{f(5) - f(3)}{5 - 3} = \frac{70 - 32}{5 - 3} = \frac{38}{2} = 19 $$

예를 들어보며 변화율을 살펴봤다. 미분은 이 변화량, 변화율 비의 극한을 의미한다고 한다.

이에 대해 알아보자

 

- x₁ = x, x₂ = x+h일 때의 변화율 그리고 h가 0에 가까워질 때

위의 예를 일반화해서 살펴보자.

 

x₁ = x, x₂ = x+h일 때의 변화율

$$ 변화율 = \frac{f(x+h) - f(x)}{x + h - x} = \frac{f(x+h) - f(x)}{h}$$

일반화해서 바라보면 위 수식과 그림처럼 변화율을 표현할 수 있다.

 

여기서 극한, h가 0에 가까워진다면 어떻게 될까?

$$ 변화율의\ 극한 = \lim_{h\rightarrow 0}{\frac{f(x+h) - f(x)}{h}}$$

 

이때, 위 수식을 실제 "f(x) = x²"을 대입해보자

$$ \lim_{h\rightarrow 0}{\frac{(x+h)^{2} - x^{2}}{h}} = \lim_{h\rightarrow 0}{\frac{x^{2}+2hx+h^{2}-x^{2}}{h}} = \lim_{h\rightarrow 0}{\frac{2hx+h^{2}}{h}} = \lim_{h\rightarrow 0}{2x+h} = 2x $$

 

h가 0이 되는 lim이기에 극한이 풀리면서 h가 사라지고 "2x"만 남게 된다.

관련해서 예시와 증명을 더 진행할 수 있지만,

중요한 것은 h(두 점의 거리)가 0에 가까워지면, "두 점간의 변화율"이 "하나의 점 x의 순간 변화율이 된다"는 것을 이해해야 한다. 그리고, 이 순간 변화율을 모든 점에 대해서 연속적으로 나타낸 것이 "도함수"이고, 예로서  증명해봤듯, f(x)=x²의 도함수는 f'(x)=2x이다.

 

그리고 우리의 똑똑한 수학자들이 도함수를 일반화해놨다. 에휴.. 아니 고마운 건가?

$$ f(x) = x^{c} \rightarrow f'(x)=c \cdot x^{c-1} $$

$$ f(x) = log_{a}(x) \rightarrow f'(x)=\frac{1}{x \cdot \ln (a)} $$

$$ f(x) = a^{x} \rightarrow f'(x)=\ln (a) \cdot a^{x} $$

$$ f(x) = sin(x) \rightarrow f'(x)= cos(x) $$

$$ f(x) = cos(x) \rightarrow f'(x)= -sin(x) $$

$$ f(x) = tan(x) \rightarrow f'(x)= sec^{2}(x) = \frac{1}{cos^{2}(x)} $$

 

- 미분의 표기

미분에는 다양한 표기법이 있지만 간단하게 살펴보고 넘어가 보자

 

$$ f(x)의\ 미분 = \frac{dy}{dx}=\frac{df}{dx}=\frac{d}{dx}f$$

 

- 미분 예제

두번째 예제는 추후 추가하겠음

 

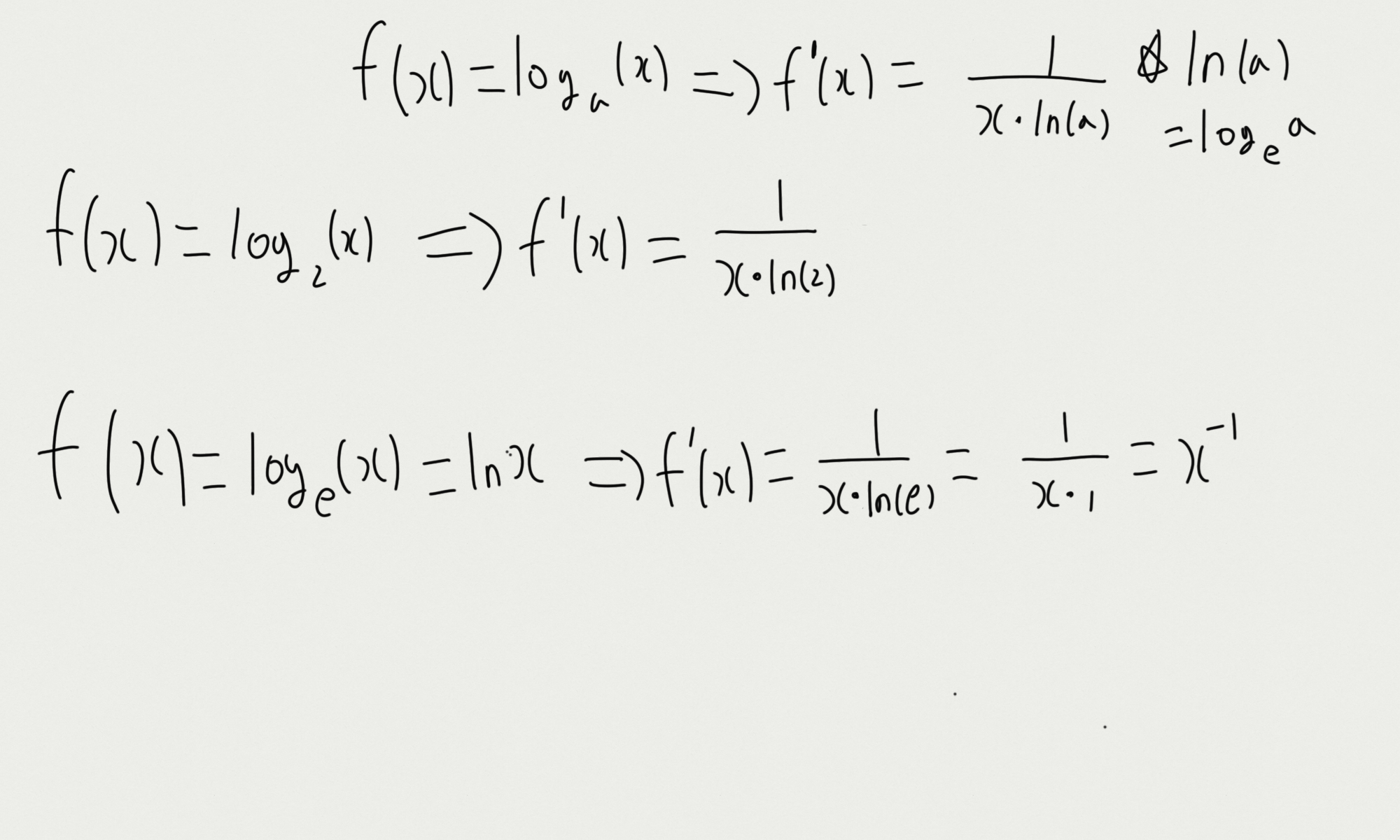
- 미분의 법칙

위키피디아에 잘 설명돼있지만, 미분은 다른 함수들과 같이 "교환 법칙", "결합 법칙"과 같은 법칙들이 성립한다. 주로 사용되는 몇 개만 살펴보자.

 

$$ 합의\ 법칙 \rightarrow (f(x) + g(x))'=f'(x)+g'(x) $$

$$ 곱의\ 법칙 \rightarrow (f(x)g(x))'=f'(x)g(x)+f(x)g'(x) $$

$$ 몫의\ 법칙 \rightarrow \left ( \frac{f(x)}{g(x)} \right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g^{2}(x)} $$

 

 

 

- 합성함수의 미분

합성함수는 둘 이상의 함수를 이어 만든 함수를 의미한다.

 

위 그림처럼 f(x), g(x)를 합성해서

x -> f(x) = y -> g(f(x)) = g(y) = z

 

x라는 input 값이 f(x)와 g(x)라는 두 개의 함수를 걸쳐 z라는 output을 얻게 된다.

이때 f(x)의 결과값이 g(x)의 input이 된다.

우리가 공부 중인 딥러닝의 chain rule과 같다.

 

그렇다고 했을 때, 이 합성함수의 미분은 어떨까?

$$ y = g(f(x))의\ 도함수 \rightarrow y'= g'(f(x)) \cdot f'(x) $$

 

위와 같은 식과 그림으로 정리된다.

 

 

 

* 참조

- https://ko.wikipedia.org/wiki/%EB%AF%B8%EB%B6%84

미분 - 위키백과, 우리 모두의 백과사전

- https://ko.wikipedia.org/wiki/%ED%95%A8%EC%88%98%EC%9D%98_%ED%95%A9%EC%84%B1

함수의 합성 - 위키백과, 우리 모두의 백과사전